[백준] 30052번: 거리 두기 게임 [C/C++]

# 문제

30052번: 거리 두기 게임
https://www.acmicpc.net/problem/30052

30052번: 거리 두기 게임

---

# 접근

문제에서 제시된 게임을 좀 더 간단히 생각해 보자.
준성이는 두 말 사이의 거리가 최대한 작도록, 효석이는 크도록 해야 한다.
효석이가 말을 어디에 두어도 자신의 말과의 거리가 D 미만이 되게 하려면, 준성이는 최대한 격자판의 가운데에 자신의 말을 놓는 것이 최선의 선택이다. 반대로 효석이는 최대한 가장자리에 말을 두어야 한다.
 
특정 경우에선 준성이가 말을 최선의 선택으로 두었을 경우 효석이는 어디에 말을 두던 두 말 사이 거리가 D 미만이 될 수 있다. 게임판 모양이 원이라고 가정해 보자.

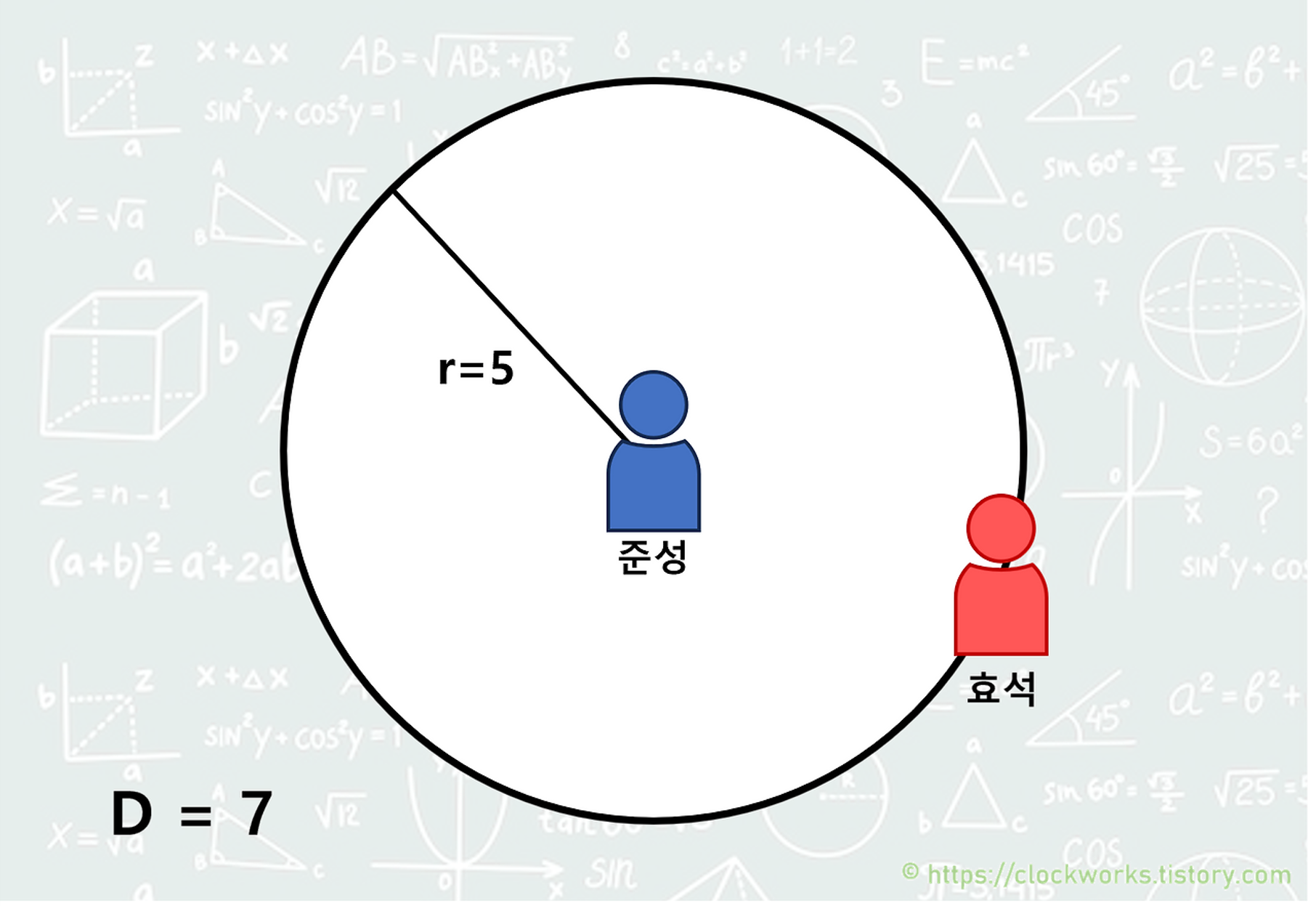
위 이미지에서 게임판은 반지름이 5인 원이고, D는 7이다. 만약 준성이가 말을 가운데에 둔다면, 효석이는 어디에 말을 두어도 두 말 사이의 거리는 D 미만이 된다.

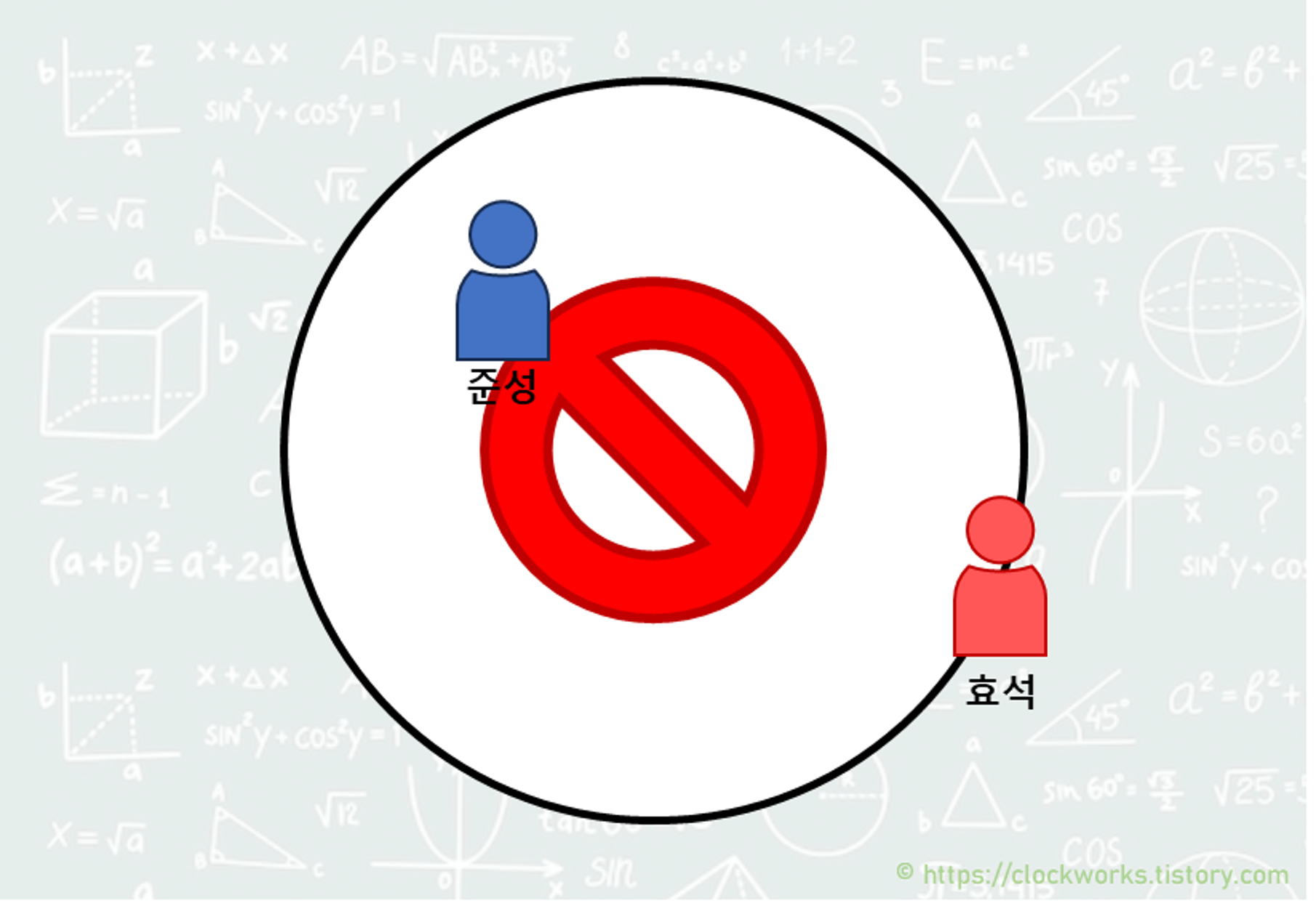
따라서 효석이는 위처럼 준성이가 말을 두기 전 말을 둘 수 없는 구역을 지정해 두 말 사이의 거리가 D를 넘도록 할 수 있다. 우리가 알고 싶은 것은 효석이가 이기기 위해 필요한 최소한의 금지 구역이다.
 
위를 통해
1. 어떤 상황에도 효석이가 둘 수 있는 최적의 자리는 격자판의 가장자리, 즉 직사각형의 4개의 꼭짓점이다.
2. 어떤 칸에 준성이가 두었을 때, 효석이가 최적의 자리에 두어도 두 말 사이의 거리가 D 미만이 되는 칸은 효석이가 필수로 말을 둘 수 없도록 설정해야 하는 칸이다.
라는 것을 알 수 있다. 즉 우리는 4개의 꼭짓점과의 택시 거리가 모두 D 미만인 칸의 개수를 세면 된다.

---

# 풀이

#include <stdio.h>

int abs(int a) { //절댓값을 구하는 함수
  a=(a<0)?-1*a:a;
  return a;
}

int main() {
  int n,m,d;
  int sum=0;
  scanf("%d %d", &n,&m);
  scanf("%d", &d);
  int arr[405][405];
    
  for (int i=1;i<=n;i++) { //왼쪽 위 모서리와의 택시 거리가 D 미만인 칸들을 1로 설정
    for (int j=1;j<=m;j++) {
      if (abs(1-i)+abs(1-j) < d) {
        arr[i][j]=1;
      }
    }
  }
    
  for (int i=1;i<=n;i++) { //오른쪽 위 모서리와의 택시 거리가 D 미만이고 1로 설정된 칸들을 2로 설정
    for (int j=1;j<=m;j++) {
      if (abs(n-i)+abs(1-j) < d&&arr[i][j]==1) {
        arr[i][j]=2;
      }
    }
  }
    
  for (int i=1;i<=n;i++) { //왼쪽 아래 모서리와의 택시 거리가 D 미만이고 2로 설정된 칸들을 3으로 설정
    for (int j=1;j<=m;j++) {
      if (abs(1-i)+abs(m-j) < d&&arr[i][j]==2) {
        arr[i][j]=3;
      }
    }
  }
    
  for (int i=1;i<=n;i++) { //오른쪽 아래 모서리와의 택시 거리가 D 미만이고 3으로 설정된 칸들의 개수를 센다
    for (int j=1;j<=m;j++) {
      if (abs(n-i)+abs(m-j) < d&&arr[i][j]==3) {
        sum++;
      }
    }
  }
    
  printf("%d",sum);
}

4개의 모서리와의 거리가 모두 D 미만인 칸의 개수를 세는 코드이다. 최종적으로 그 개수가 답이 된다.